|
[next]
[previous]
[up]
Abstract
"An Account of Regge Asymptotics of the Scattering Cross-Section In the
Theory of Multiple Scattering in Amorphous Media"
N. V. Bondarenko
Department of Physics and Technology, Kharkov State University,
31 Kurchatov Avenue, Kharkov, 61108, Ukraine
E-mail:bon@kipt.kharkov.ua
The Bethe-Moliere theory of high-energy multiple scattering is revised.
Consequences of introducing to the theory of Regge asymptotic behaviour for
an elementary cross-section,
 (q) ~ q-4+4 (q) ~ q-4+4 , ,
 > 0
are analysed. It is shown, that replacing the logarithmic behaviour by a
power one leads to a formula for for the distribution function in the form
of a certain integral, which is positive and monotonic function of q.
That can be regarded as an improvement as compared with the Bethe-Moliere
expansion, which when cut off can give a negative probability. We argue,
that the right way of approaching the singular point > 0
are analysed. It is shown, that replacing the logarithmic behaviour by a
power one leads to a formula for for the distribution function in the form
of a certain integral, which is positive and monotonic function of q.
That can be regarded as an improvement as compared with the Bethe-Moliere
expansion, which when cut off can give a negative probability. We argue,
that the right way of approaching the singular point
 = 0
is from the side of positive values, and it turns out, that in this limit = 0
is from the side of positive values, and it turns out, that in this limit
 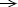 +0
the theory as whole does not turn into the Bethe-Moliere
one. In the area of single scattering (q) we obtain a linear growth
with time, that seems more natural, then the logarithmical evolution in the
Bethe-Moliere theory. +0
the theory as whole does not turn into the Bethe-Moliere
one. In the area of single scattering (q) we obtain a linear growth
with time, that seems more natural, then the logarithmical evolution in the
Bethe-Moliere theory.
|
[next]
[previous]
[up]
|
 (q) ~ q-4+4
(q) ~ q-4+4 ,
,
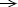 +0
the theory as whole does not turn into the Bethe-Moliere
one. In the area of single scattering (q) we obtain a linear growth
with time, that seems more natural, then the logarithmical evolution in the
Bethe-Moliere theory.
+0
the theory as whole does not turn into the Bethe-Moliere
one. In the area of single scattering (q) we obtain a linear growth
with time, that seems more natural, then the logarithmical evolution in the
Bethe-Moliere theory.